Measuring ‘engagement’ on social platforms is always going to be a proxy for an actual concept of value; a user engaging with something doesn’t mean they value it. This paper closes that gap, connecting engagement behaviors to value through a Bayesian network. The authors implement their approach on Twitter.
Authors: Smitha Milli, Luca Belli, Moritz Hardt
Link: arXiv; to appear at FAccT 2021.
Background and motivation
From the abstract:
Most recommendation engines today are based on predicting user engagement, e.g., predicting whether a user will click on an item or not. However, there is a potentially large gap between engagement signals and a desired notion of value that is worth optimizing for.
Put otherwise, this is a classic case of the proxy problem; engagements are a proxy for value, but the two are not the same. Engagement can be negative, and different types of engagement (adding a Netflix video to My List vs. watching it) can provide different indications of value.
This paper attempts to operationalize the idea of value. They do this in three ways:
-
Using measurement theory to aggregate engagement signals into an objective function to capture “value.”
-
Creating a latent variable model for this use case, and showing how to identify it.
-
Implementing and qualitatively evaluating this approach on Twitter (referred to throughout as “the Twitter platform”).
Latent variable model and Bayesian network
Suppose that you have a set of behaviors $B$—on Twitter, retweets, likes, replies, etc.—which provide signals for “value.” If you operationalize value as a binary latent variable $V$, then you want to be able to measure $P(V = 1 | B)$. Measuring this accurately lets you replace any existing objective focused on engagement.
The authors’ insight comes from an anchor variable $A$, from which you can identify $P(V = 1 | A = 1)$. An anchor should be an action for which you have “strong, explicit feedback from the user.” Downvoting or saying “I don’t want to see this” are examples of negative feedback, for which you can assume $P(V=1|A=1) = 0$. Likewise, upvoting or retweeting are positive feedback.
The system is modeled as a Bayesian network. The network consists of the relationships between different behaviors. For example, clicking on a tweet is necessary to retweet it or reply to it. The goal is to determine $P(V|A, B)$.
The anchor variable $A$ must:
- carry signal about the value
- not have any children (no behaviors can depend on the anchor)
- give information about the value that does not depend on the parents (it’s a strong type of feedback)
The authors specify how the objective $P(V|A, B)$ can be determined from known or inferrable distributions. Some are simple—$P(V)$ is just a prior, $P(A,B)$ is empirical—and some are more complex, requiring heuristics that are application-dependent.
Application: a Twitter case study
My favorite part of this paper is that the authors applied it directly to Twitter. They used this to measure the value of different machine learning-based notification systems. The motivation for this is excellent:
On Twitter, there are many kinds of user behaviors: clicks, replies, favorites, retweets, etc. The typical approach to recommendations would involve optimizing an objective that trades-off these behaviors, usually with linear weights. However, designing an objective is a non-trivial problem. How exactly should we weigh favorites compared to clicks or replies or retweets or any of the numerous other behaviors? It is difficult to assess whether the weights we chose match the notion of “value” we intended.
Furthermore, even supposing that we could manually specify the “correct” weights through laborious trial-and-error, the correct weights change over time. For example, after videos shared on Twitter began to auto-play, the signal of whether or not a user watched a video presumably became less relevant. The reality is that the objective is never static - how users interact with the platform is constantly changing, and the objective must change accordingly.
Using this approach, however, the authors operationalize value as a latent variable defined by an anchor and various behaviors. Here, the anchor is the “see less often” button on a tweet, which is strong, explicit, negative feedback.
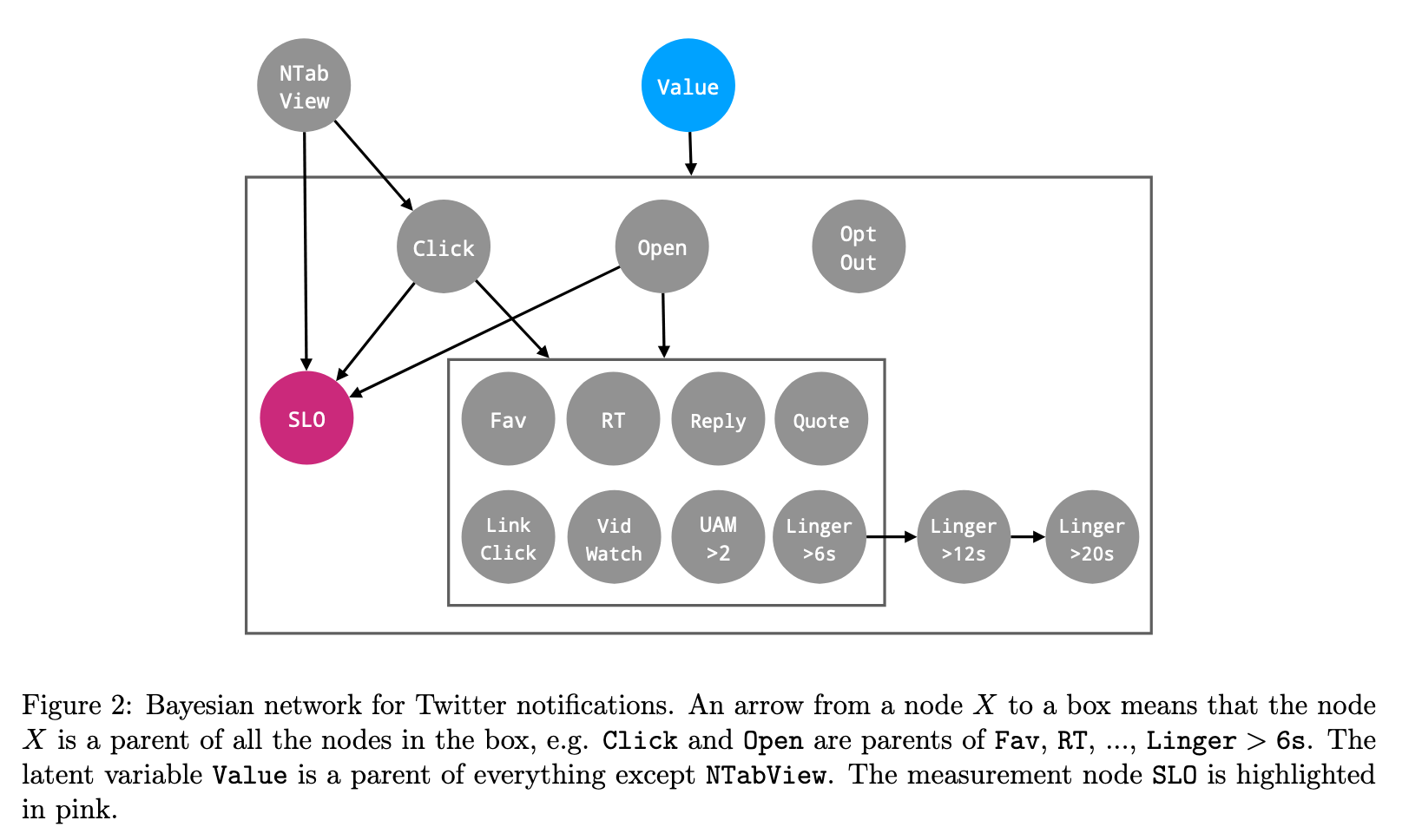
The goal is to estimate the value of different notifications (NTab View in the image).
If a user sees a notification in NTab View, they might Click it to get to the tweet, then possibly favorite, retweet, or linger on it.
Meanwhile, Open just refers to opening the app from the home screen.
The Value node is a latent parent of all possible behaviors.
The OptOut node (opting out of notifications) is assumed to be attributed to any ML-based notifications that came in the past day.
Finally, the anchor SLO (see less often) can be caused by the notification view or clicking or opening a tweet.
Evaluation
How do you evaluate something like this? Reporting engagement metrics isn’t enough; the point of this paper is that value is different from engagement. But value is also latent.
Here, the authors evaluate “evidence based on internal structure, i.e., whether expected theoretical relationships between the variables in the model hold.”
They evaluate P(V = 1 | Behavior = 1) for different individual behaviors (marginalizing over all other variables).
They compare their Bayesian network to a naive Bayes model and a simpler variant of their network.
The authors find that all behaviors that they expect to increase the probability of a value do so. The relative strengths make sense, too: $P(V = 1 | RT = 1) > P(V = 1 | LinkClick = 1)$. They find other inferences which would be indiscernible from a more theoretical approach.
How do you assess validity? I won’t summarize this, but there’s a great discussion of how the five categories of evidence for validity (from Standards for educational and psychological testing) translate into the recommender system setting.
Discussion
This was an excellent paper. The authors did a great job of motivating the relevant probability theory and providing intuitive explanations. The application was direct and occurred in a real environment.
A lot of the novelty here comes from decomposing this abstract idea into tractable elements. When I was working with Bayesian networks and high-dimensional joint distributions, my biggest challenge was breaking down the complicated network structure into simpler, tractable pieces. That the authors managed to do so in a real, large-scale application is impressive to me.
I noticed that all of the posterior probabilities for $P(V = 1 | Behavior = 1)$ were greater than the prior of 0.5. That is, this model learned that any of these behaviors were evidence that a notification provided value (besides opting out of notifications, which is an extreme action).
Is this a self-fulfilling prophecy? The authors included many positive behaviors and then found that they predicted value to a user. That makes sense, but it makes me wonder if there are more negative behaviors that could have predicted a lack of value: unfollowing a user, quickly exiting a tweet, closing the app shortly after, etc.
Part of this relates to Twitter’s design. There are not many negative signals I can send, besides the nuclear “see less often.” The authors note that this matters, though they don’t discuss whether or not Twitter meets this design goal:
What content-based evidence makes clear is that to measure any worthy notion of “value”, it is essential to design platforms in which users are empowered with richer channels of feedback.
I’m reminded of Eugene Wei’s Seeing Like an Algorithm, which discusses how the design of TikTok gives clear, immediate signals about a user’s feelings about a video. Twitter doesn’t really do this. My feed usually has a few tweets at once, and if I’m scrolling through them without clicking on any, I’ll like some and dislike others and Twitter will never be any wiser for it.
On the whole, this paper was great. I would love to work at a company or in a research group where I could develop and prototype ideas like this. This paper gave me one of the clearest “I would love to do this” signals I’ve noticed. I look forward to seeing more discussion of it as FAccT 2021 happens in a couple months.
