This Google Brain paper from ICLR 2017 tackles the question of generalization in neural networks. What causes a network that performs well on training data to also perform well on testing data? (Answer: ¯\_(ツ)_/¯)
Authors: Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, Oriol Vinyals
Link: arXiv
Central results
The abstract, broken down:
- conventional deep learning wisdom “attributes small generalization error either to properties of the model family, or to the regularization techniques used during training.”
- they do “extensive systematic experiments”
- and find that the above explanation does not hold in practice
- in particular, a CNN can “easily fit a random labeling of the training data”
- and that happens even if the images are replaced by noise.
The central finding of this paper is that “deep neural networks easily fit random labels,” contradicting conventional wisdom about model architectures, model size, hyperparameters, or optimization.
They went beyond random labels to random noise. CNNs could fit images that were entirely Gaussian noise with zero training error. And when varying the amount of noise (interpolating between no noise and all noise), they observed a “steady deterioration of the generalization error as we increase the noise level.”
This implies:
- model architecture is not enough to explain generalization
- explicit regularization is not enough to explain generalization
- theoretically, a two-layer ReLU network with 2n + d parameters can express any labeling of n samples in d dimensions
- stochastic gradient descent acts as an implicit regularizer
Wow—crazy stuff.
Experiments
They run a bunch of experiments on CIFAR10 and ImageNet, standard image classification datasets:
- true labels
- partially corrupted labels (with probability p, the label is replaced by another one)
- random labels (they’re all random)
- shuffled pixels (the pixels in every image are permuted in the same way)
- random pixels (the pixels in every image are permuted in a different way)
- Gaussian (pixels are generated according randomly to a Gaussian distribution)
The networks they test—Inception v3, AlexNet, and a couple garden variety MLPs—can fit both the original and random labels with 100% training accuracy. An abridged version of Table 1 in the paper:
| model | dataset | train accuracy | test accuracy |
|---|---|---|---|
| Inception | CIFAR10 | 100.0 | 89.05 |
| Inception | CIFAR10, random labels | 100.0 | 9.78 |
| AlexNet | CIFAR10 | 99.90 | 81.22 |
| AlexNet | CIFAR10, random labels | 99.82 | 9.86 |
| MLP 3x512 | CIFAR10 | 100.0 | 53.35 |
| MLP 3x512 | CIFAR10, random labels | 100.0 | 10.48 |
| MLP 1x512 | CIFAR10 | 99.80 | 50.39 |
| MLP 1x512 | CIFAR10, random labels | 99.34 | 10.61 |
Abridged Table 1: the training and test accuracy of various models on CIFAR10
Some of these results also show up in Figure 1. This Figure also demonstrates that networks can always fit corrupted training sets perfectly, but the test (generalization) errors approach 90%, equivalent to random guessing.
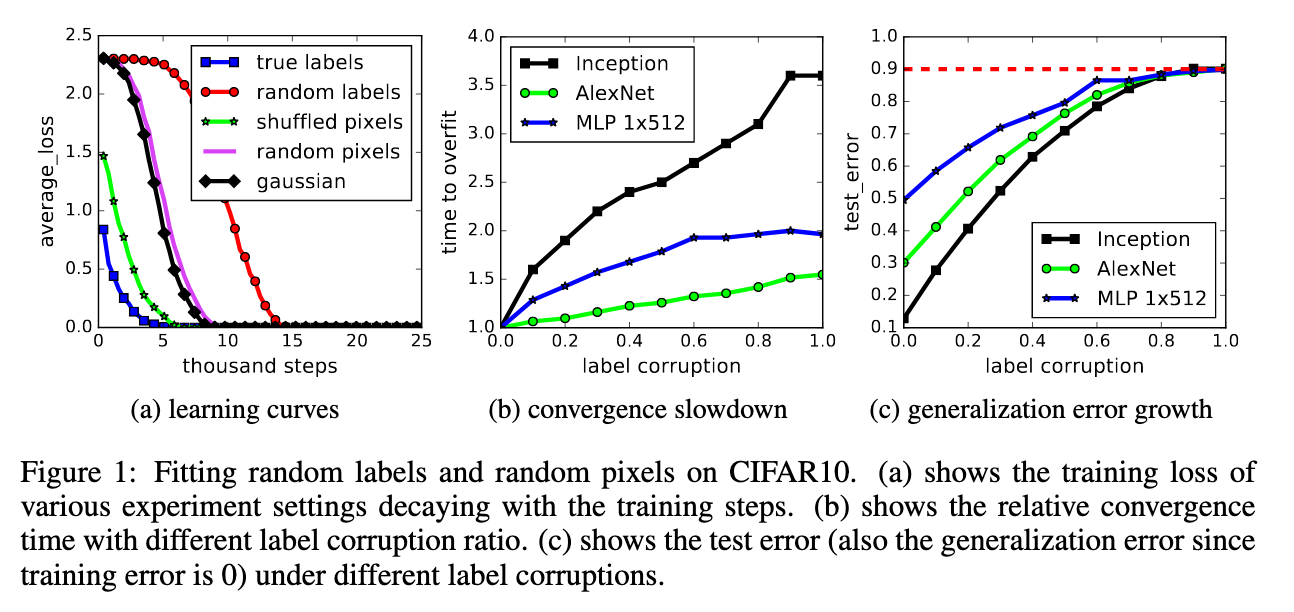
This leads to a range of intermediate learning problems where there remains some level of signal in the labels. We observe a steady deterioration of the generalization error as we increase the noise level. This shows that neural networks are able to apture the remaining signal in the data, while at the same time fit the noisy part using brute-force.
On regularization
The idea behind regularization, both in theory and in practice, is to help mitigate overfitting. You “confine learning” to a lower-complexity region of training space. Regularization techniques are their own subfield of machine learning research.
This paper studies:
- data augmentation: adding transformations (random cropping, random perturbations of hue or saturation, etc.) to the training set
- weight decay (or L2 regularization)
- dropout (mask each weight randomly to zero with some probability)
Their basic conclusion (though I didn’t spend as much time understanding this) is that explicit regularization helps improve generalization, but is not necessary for it.
Implicit regularization (early stopping, batch normalization) similarly helps, showing that “early stopping could potentially improve the generalization performance” and “the [batch] normalization operator helps stabilize the learning dynamics.”
In summary, our observations on both explicit and implicit regularizers are consistently suggesting that regularizers, when properly tuned, could help to improve the generalization performance. However, it is unlikely that the regularizers are the fundamental reason for generalization, as the networks continue to perform well after all the regularizers removed.
No easy answers here!
Finite sample expressivity
Research on the “expressivity” of neural networks studies what classes functions (of an entire domain‚ can(not) be represented by certain classes of networks. The authors study expressivity of samples.
The key result is that: for n samples in d dimensions, there exists a two-layer ReLU neural network with 2n + d weights that can represent any function on those samples. If you’d rather the network be wide than deep, you can have width O(n/k) and depth k. I didn’t (try to) understand the proof.
Thoughts
I’m not very familiar with the pure machine learning world that this paper sits in. But the results don’t seem that surprising to me, which makes me feel like I’m missing something. I thought it was known that neural nets could express any function, and so the fact that they can memorize random labels is bad but not surprising.
I think this paper was exceptionally well-written. It appears to have been impactful (it’s been cited ~2000 times in 3 years) while also being easy to read. While I skipped the proofs in the appendix, the main results were clearly presented and the structure of the paper (with a lengthy introduction) was helpful.
Where does this leave us, in terms of “rethinking generalization”? The authors claim that it means existing statistical learning theory is inadequate why neural nets do and do not generalize. I am not sure I understand this point.
Some resources I used while reading this were The Morning Paper and Daniel Seita’s blog.
